1. The probability that a light switch will work at the nth demand is 0. 9999/n^(1/n).
The switch is used 2 times per day.
What is the probability that the switch will fail during the first five days following installation?
A. 0.068
B. 0.875
C. 0.932
D. 0.75
Solution: The switch must have worked at all the previous n-1 demands for the switch to work at the nth demand.
Let Dn: Light switch operates at the nth demand
and Wn: Light switch operates for each of the n demands.
The probability that the switch does not fail during the first five days of installation is:
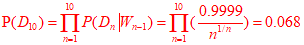
Then, the probability that the switch fails during the first five days = 1-0.068 = 0.932
2. For the exponential distribution, any mean life value determines a life for a specified value of R; i.e., the reliable life may be established for any mean and desired reliability. Thus it is more meaningful to set a reliability goal in terms of a statement that a “0.xx reliability for 1000 cycles of operation is required”. So, if the mean number of cycles to failure is 1000, what is the 0.95 reliability for 1000 cycles of operation?
A. 9491 cycles
B. 6153 cycles
C. 99499 cycles
D. 19496 cycles
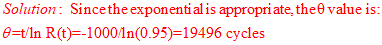
3. Suppose one knew that the failure process of a device was such that essentially all of the devices would fail before 10000 hours, but that 95% of the devices would operate beyond 2000 hours. Further, it is known that the failure times follow a normal distribution.
In this case, it is known:
A . μ=4700, σ=1722,
B. μ=4833, σ=1650,
C μ=4833, σ=1722,
D. μ=1722, σ=500,
4. What does Step-stress testing NOT do :
A. Tests initially at operating stress, then stress is increased step-wise
B. Increase stress level until failure
C. Used to project reliability in use condition
D. Plot failures as a function of stress-time
5. The times to failure for a machine used in surface mount technology follows a Weibull distribution with
β=2, η=30 weeks. a) What is the probability of surviving 40 weeks? And
b) What is the probability of the machine failing in the interval (40,50) weeks?
A. 0.169, 0.4302
B. 0.169, 0.158
C. 0.169, 0.5625
D. 0.144, 0.4302
Solution:
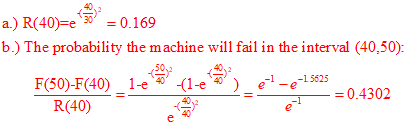
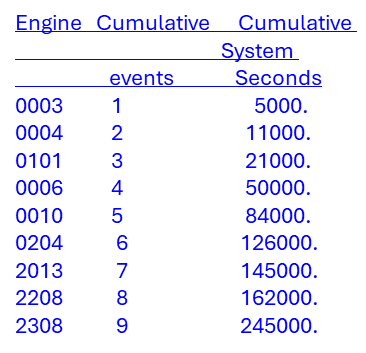
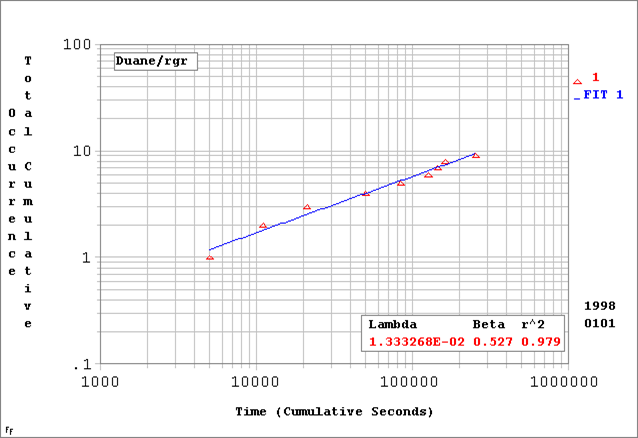
6. Using the rocket data in this table, Calculate the projected instantaneous
failure rate at 1,000,000 seconds of maturity.
A.0.85/100K sec
B. 0.94/100K sec
C. 0.75/100K Sec
D. 1.32/100K Sec
Solution: Inst f.r. @1,000K sec=(1.333E-02*(1,000,000.527)/1,000,000)*.527= .94/100,000sec
7. An engine bearing is redesigned due to multiple unbalance events. A Weibull distribution of the original bearing failures resulted in a b = 2 and h = 600 hours. You have 5 redesigned bearing systems to test. How long must you test these redesigned bearings to have 90% confidence that the failure mode has been corrected?
A. 455 hrs each
B. 407 hrs each
C. 317 hrs each
D. 691 hrs each
Solution: see USAF Weibull Handbook page 91,
or solve for t:
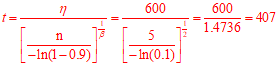
8. The PDF for the time-to-failure of an appliance is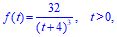 
where t is in years
Find the reliability R(t), then using R(t), Find the failure rate λ(t).
A. λ(t)=2/(t+4)
B. λ(t)=3/(t+4)
C. λ(t)=1/(t+4)
D. λ(t)=16/(t+4)
Solution:
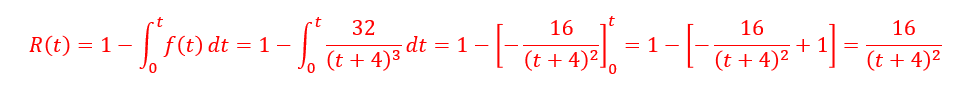
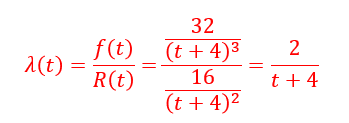
9. The failure rate on a new brake drum design is estimated to be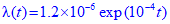 
per set, where t is in kilometers of normal driving. Forty vehicles are each test-driven for 15,000 km.
How many failures are expected, assuming that the vehicles with failed drives are removed from the test?
A. 1.5
B. 1.44
C. 2.12
D. 1.67
Solution: Probability of failure in 15,000 :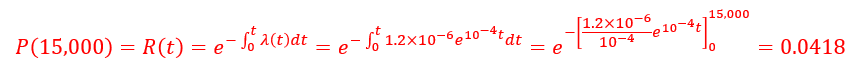
Therefore, # of expected failures in 15,000 mile=40×0.0418= 1.67
10. In fault tree analysis, what logic gate is represented by the probability expression of PT = P1 + P2 – P1P2?
A. INHIBIT gate
B. OR gate
C. AND gate
D. INHIBIT + and GATES